伊藤園の「株価」は「気温」と関係ある？〜ラグ相関編〜

はじめに

毎回同じ説明になりますが、

• 暑ければ飲み物を飲むよね？
• 寒ければ飲み物を飲まないよね？

と思い、気温と飲料メーカーの株価に関連があれば面白いなーと思い、始めてみました！

株価はそんな単純なものではないので、少し関連しているという結果が出たら嬉しいなぁといった軽い気持ちでやっています。

お馴染みの、伊藤園(2593)を対象とします。

データ・手法

使用データ

今までと全く同じですが、初見の方のためにもう一度説明します。

比較対象として使用する伊藤園の株価データは、Stooqから取得した１日ごとの終値を使用しました。

また、気温のデータは気象庁から取得した東京の日平均気温、日最高気温、日最低気温を使いました。

期間はいずれも2013年１月１日から2020年12月31日の８年間です。

データの種類	取得元	内容
株価	Stooq	終値
気温	気象庁	日最高気温 日平均気温 日最低気温

手法

今回はラグ相関を計算します。

ラグ相関とは、一方をずらして計算した相関係数のことです。

今回のパターンに当てはめて説明すると、その日の株価と何日か後の気温の相関係数を計算するということです。

そのため、データ数が一致しないので、データがずらした日数分少なくなっています。

気温データは毎日存在するのに、株価データは土日が存在しないため、計算めんどくさかった笑

計算ミスはきっとしていないはず・・・

手法を順序立てて説明します。

1. 気温のデータを該当日数分ずらして、株価データと対応させる。
2. 株価データに線形トレンドの除去をする。
3. 相関係数を計算する。

相関係数やトレンド除去がわからない方は、前回の記事を参照してください。
トレンド除去した後にデータを形成させた方が実際は良いのですが、大きな誤差を生まないと思ったのでこのようにしました。

（除去するトレンドの日数が一致していないため）

今回は、30日から180日まで30日ずつずらした６パターンで計算しています。

スポンサーリンク

結果

ラグを作った株価と気温の経年変化

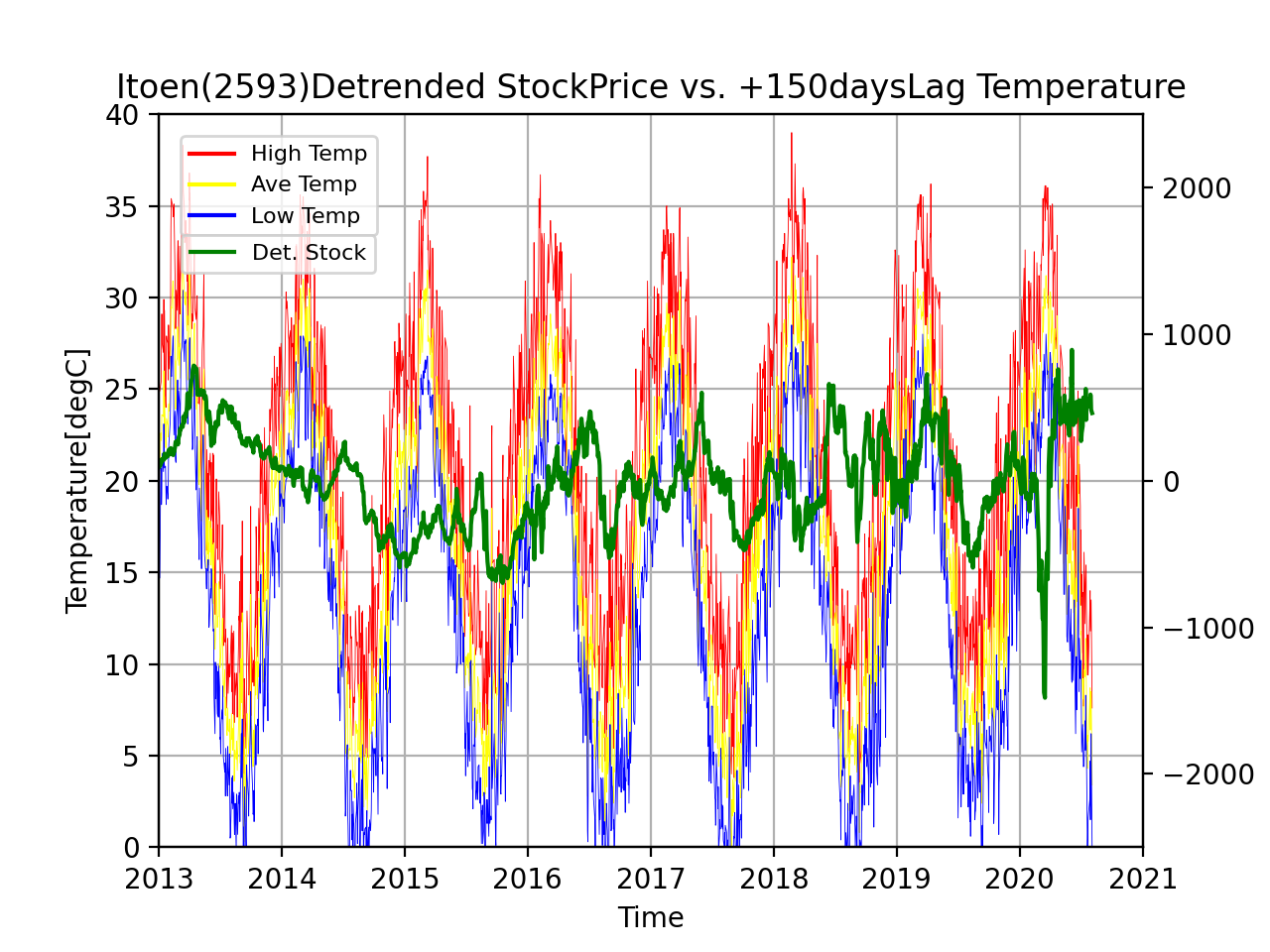
まず図を載せます。枚数が多い。。。

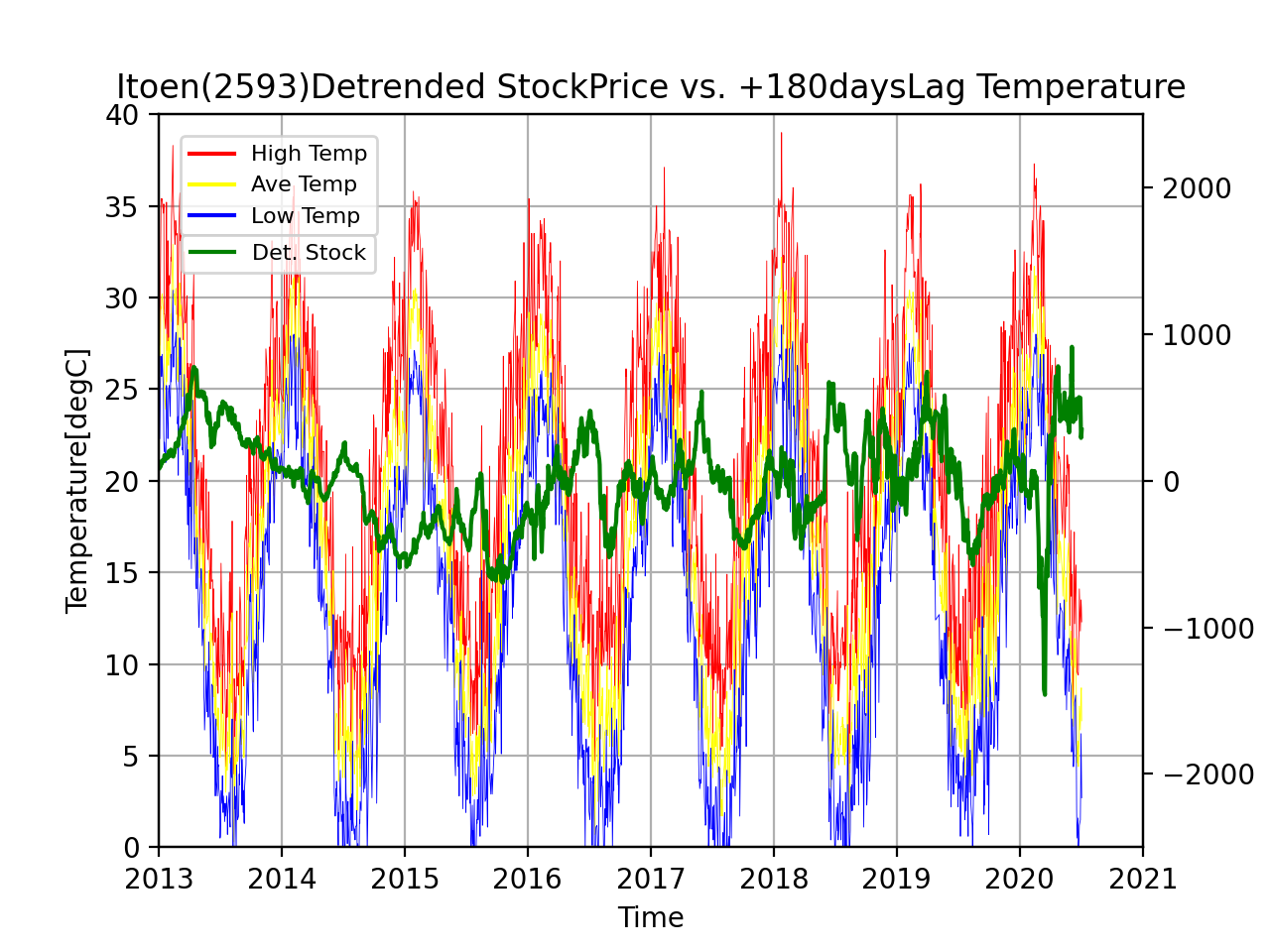左上：30日、右上：60日、左：90日、右：120日、左下：150日、右下：180日ずらしたグラフです。

線はそれぞれ、トレンド除去した株価、該当日数ずらした最高気温、該当日数ずらした平均気温、該当日数ずらした最低気温です。

少しわかりにくい図ですが、30日ずらした図の場合、１月31日の気温をグラフ上の１月１日に描画しています。

図を眺めてみると、以前よりも関係ありそうな感じがしてきませんか？

それでは、実際にラグ相関係数を見ていきましょう！

以下は、便宜上

• トレンド除去をした株価：株価
• ずらした気温：気温

とします。

スポンサーリンク

対象期間全体での相関係数

まずはいつも通り、全期間での相関係数を計算しました。

以後、結果は小数第４位を四捨五入した値を示しています。

今回の計算でわかることは、少し難しいですが、株価が長期的なトレンドに比べて、どれだけ○日後の気温に左右されやすいかです。

正の相関がある場合は、長期的な傾向よりも株価が上がった場合に、○日後の気温も上がっているということです。

結果を下の表にまとめます。
すごく多いですが、お許しを。

ずらした日数	最高気温	平均気温	最低気温
30日	0.147	0.160	0.164
60日	0.231	0.247	0.251
90日	0.223	0.246	0.255
120日	0.185	0.203	0.214
150日	0.003	0.029	0.044
180日	-0.146	-0.136	-0.126

意外と高くない？？

関係あると言うには低い数値とはいえ、やはり株価は未来の予測値が入っていることが感じられます。

前回までは0.1にも満たしていなかったので、これはもしかすると・・・？

特に、60〜120日に期待が持てますね。

また、180日（半年）で負の相関が少し出るのは、半年経つので厳しい季節になるほど株価が上がるから？

（180日の負の相関は、現在が夏の場合、冬の気温が下がる方が株価が上がる、一方、冬の場合は気温が上がる方が株価が上がる）

これも興味深いですね。

季節ごとで分けた場合

今度は、季節ごとに分けて、ラグ相関係数を計算します。

季節の定義はいつも通りの以下です。

• 春：３月〜５月
• 夏：６月〜８月
• 秋：９月〜11月
• 冬：12月〜２月

量が多いですが、頑張ってついてきてください。

今回欲しい値は、相関係数が０から離れた値だけなので、０に近い値は無視することで理解しやすくなるはずです。

それでは結果に移ります。

春（３月〜５月）

ずらした日数	最高気温の相関係数	平均気温の相関係数	最低気温の相関係数
30日	0.151	0.221	0.250
60日	0.104	0.163	0.203
90日	0.073	0.121	0.155
120日	0.184	0.176	0.160
150日	-0.178	-0.152	-0.132
180日	-0.191	-0.212	-0.235

ずらした日付が120日までは、正の相関が0.2(4%)あるのかないのかで推移しており、

150日以降は0.2(4%)程度の負の相関になっています。

最高気温よりも平均気温や最低気温の方が、相関が高い傾向ですね。

夏（６月〜８月）

ずらした日数	最高気温の相関係数	平均気温の相関係数	最低気温の相関係数
30日	0.198	0.227	0.228
60日	0.266	0.295	0.287
90日	0.297	0.328	0.325
120日	0.193	0.230	0.238
150日	0.243	0.252	0.230
180日	-0.053	-0.032	-0.021

これは結構嬉しい結果となりました！

ずらした日数が150日までは約0.2(4%)の正の相関が続いています。

特に90日では、0.3(9%)を越えました。

春と同様に、最高気温ではなく、平均気温や最低気温で高くなりがちなのは、よく覚えておいてください。

スポンサーリンク

秋（９月〜11月）

ずらした日数	最高気温の相関係数	平均気温の相関係数	最低気温の相関係数
30日	-0.117	-0.130	-0.141
60日	0.027	0.014	0.003
90日	0.010	0.018	0.015
120日	0.121	0.162	0.189
150日	0.053	0.082	0.111
180日	0.091	0.111	0.127

大した結果なし！次！

冬（12月〜２月）

ずらした日数	最高気温の相関係数	平均気温の相関係数	最低気温の相関係数
30日	-0.008	0.051	0.104
60日	0.077	0.115	0.126
90日	0.057	0.094	0.010
120日	-0.005	0.020	0.049
150日	0.040	0.083	0.096
180日	0.041	0.076	0.097

冬場も何かしらの傾向が出るかと思ったら、微妙ですね。

冬は温かい飲み物が売れやすい？とか気温が高い方が飲み物売れがち？とか

思いましたが、未来の気温には左右されないようですね。

考察

今回得られた明確な結果として、

• 春の株価が120日までは正の相関、150日以降は負の相関
• 夏の株価は150日まで正の相関

がありました。

この２点について、私なりの解釈を説明します。

春の株価とずらした気温に正と負の相関がある理由

春は相関係数は0.2(4%)程度ですが、ずらした日数が120日まで正の相関、150日以降は負の相関が現れました。

まず、120日までの正の相関の理由について。

120日までは春から９月までにあたりますが、その期間にかけていつもより気温が上がると予想されると、飲み物がいつもより多く売れる可能性が高いことになります。

即ち、気温がいつもより高くなる見込みがある影響で、株価が上がるのではないかと思います。

夏場は暑いと沢山飲み物が欲しくなりますからね。

想像と結果が一致しているのと思います。

一方で、秋に差し掛かる150日以降までいくと、負の相関ということで、気温が下がる見込みがあるほど、株価が上がりやすい傾向になるということですね。

これは正直よくわかりませんが、秋にかけての期間なので、冬に寒くなる前触れ？を示しているような気がします。

即ち、異常な気候になりやすい見込み（夏はより暑い、冬はより寒い）があるなら、株価が上昇しやすいのかな？と思います。

そもそも180日先の気温なんて予測が困難だからどうなんだろ・・・。

また、平均気温や最低気温が最高気温よりも結果が明瞭になった理由としては、１日中暑い方が飲み物を飲みやすいからかなと考えています。

昼間に気温が急上昇するパターンよりも、午前中や夕方から暑い方が厄介で、昼間だけ暑い時よりも飲み物を飲みたくなるという考えは、自然な気がします。

夏の株価とずらした気温に正の相関がある理由

夏では、ずらした日数が150日までに、正の相関が0.2を超えたパターンが多くありました。

その中でも、0.3(9%)を超えた90日が最も良い結果でした。

春の結果とは反対に、夏の結果は秋から冬にかけて気温が上昇していたら、株価が上がるという事ですね。

話は変わりますが、最近秋がすごく短くなったなぁって思いませんか？

最近の秋は、９月や10月でも気温が物凄く高く、秋が来た気分になれないんですよね。

話を元に戻すと、今回の結果はこの秋の気温が下がらないことを示しているのだと思います。

即ち、秋もいつもより気温が高いと予想されれば、夏と同水準程度に飲み物が売れ続けるはずなので、それを株価が反映しているのではないかと考えています。

最低気温や平均気温が最高気温よりも結果が明瞭なのは、春のパターンと同じです。

１日中暑い方が、きっと飲み物は売れるはずです。

注意点

今回、上記のような結果が出ましたが、必ずしも株価と気温が関連していることを示すものではありません。

どういうことかというと、例えば、以下のことが挙げられます。

• 株価と経済成長に相関がある
• 経済成長と気温に相関がある

上記のどちらも当てはまっていた場合、株価と気温が関連していなくても、どちらも経済成長に関連した動きとなるので、相関が出てしまいます。

例として経済成長を挙げましたが、株価と気温の間に関連する何かがもしかするとあるかもしれません。

このような見かけの相関のことを疑似相関と言います。

疑似相関の可能性が０ではないため、その点はご承知おきください。

まとめ

↓とりりんを応援して頂けると嬉しいです！↓

にほんブログ村