こんにちは、とりりんです。
今日はデータに存在する周期を調べる手法であるFFTについて簡単に紹介します。
これからFFTをたまに使っていこうと思っているのですが、理解して頂くために本記事を書きます。
- FFTをすることで何がわかるのか知りたい
- 本ブログのこれからの解析記事を理解したい
FFTとは
FFTとは、Fast Fourier Transformの略で、高速フーリエ変換と呼ばれる解析手法です。
この手法により、データにどの周期帯が卓越しているかを知ることができます。
与えるデータが波形の足し合わせでできていると仮定して、データがどのような波形で構成されているかを示すための手法です。
例えば、気温の時系列データには1日単位の波形のみであるため、FFTをすると1日周期のみが卓越していることがわかります。
本ブログでは、主に株価が何らかの周期的な現象をしているかを調べることを目的に、FFTを使う場面が多くなると思います。
これだけだと全くわからないと思うので、例を見ながら理解していきましょう。
1つの波形に対するFFT
まず、例のデータとするサインカーブをお見せします。
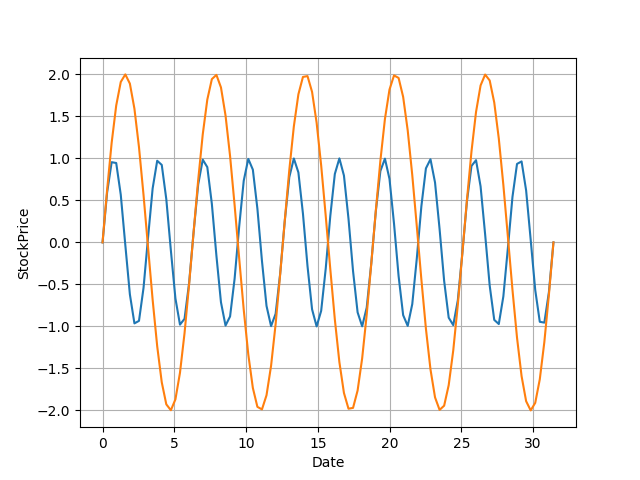
下図は横軸が時間、縦軸は株価(株価に負はないんだけど)のsin(2x)と2sin(x)のサインカーブを示しています。
縦軸は任意の要素だと思ってください。
このデータ中に、sin(2x)は10個の周期(10回繰り返されている)、2sin(x)は5個の周期が存在しているのが分かりますよね。
この例のデータの場合、綺麗な波形をしているため、FFTによって変な要素が拾われずに存在している周期が取り出せたら正解となります。
では、このデータにFFTをした結果が下図です。
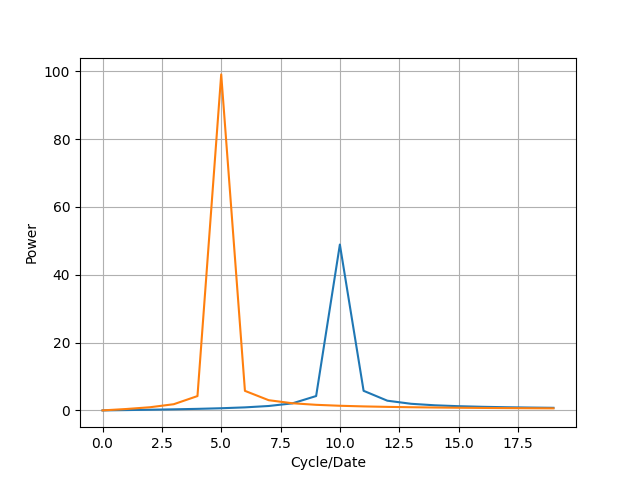
この図は、横軸がデータ内に存在する周期の数、縦軸がその周期帯の強さ(パワー)を示しています。
この図はどういうことかと言うと、sin(2x)の変化では、データ内で5個周期を持つ波形はかなり弱い(横軸が5の位置ではパワーがほぼ0)、10個周期を持つ波形はかなり強い(横軸が10の位置でグラフが飛び出ている)ことがわかります。
そのため、sin(2x)はほぼ10個周期の要素だけが存在していることがわかります(求めている結果ですよね)。
また、sin(2x)よりも2sin(x)の方がパワーが大きいですよね。
これは、波形の振幅が大きい方が、パワーが大きくなるからです。
スポンサーリンク
複数の波形を重ねた場合
次に、先ほどの2つの波形を足し合わせた場合について考えます。
足し合わせた図は下のようになります。
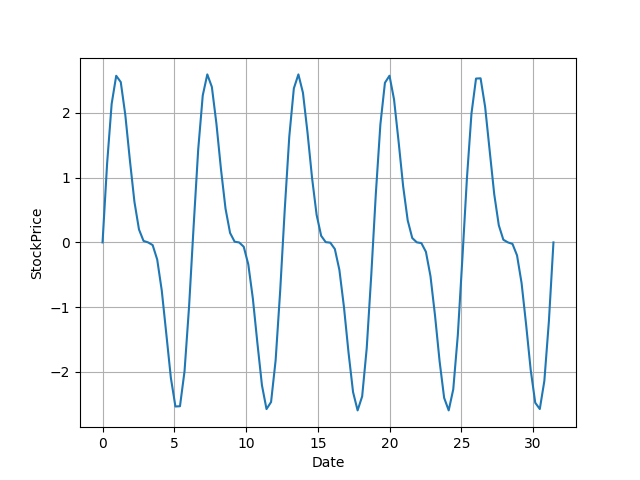
なんか繰り返されている感じはありますが、綺麗な波形では無くなりましたよね。
これにも同様にFFTをしてみましょう。
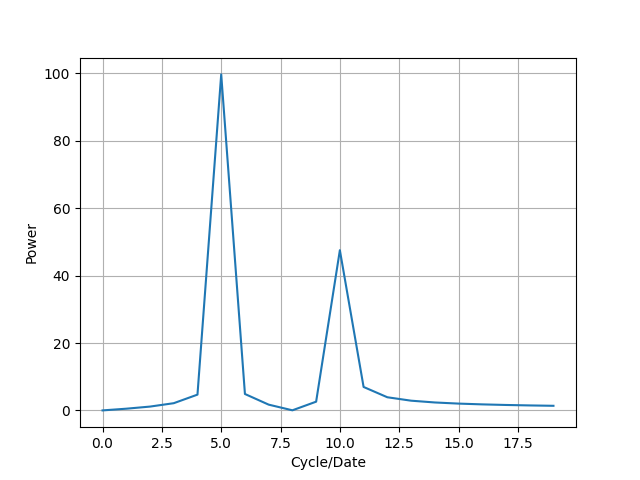
凄くないですか!?
10個周期なんて見た目だと全然わからないのに、しっかり5個周期と10個周期が取り出せています。
5個周期の方が振幅が大きいこともちゃんと表されていますよね。
このように、FFTを実行するデータは各波形が重ね合わされていると仮定して、FFTで卓越している周期が取り出せるのです!
これを踏まえて、株価のような更に複雑な時系列データにFFT解析をすることで、チャートで見えなかった隠れた周期を取り出すことができるかもしれません。
現実の株価などのデータは、今回のようにわかりやすいデータではないため、綺麗に取り出すことは難しいですが、この手法により大きな現象に隠れている弱い周期みたいなものは取り出せると思っています。
まとめ
今日は、周期を取り出す手法であるFFTについて解説しました!
やろうとしていることは理解していただけたでしょうか?
今後、FFTを使った解析をしていく予定ですので、是非頭に入れておいて頂けると嬉しいです。
最後までご覧いただき、ありがとうございました!
↓とりりんを応援して頂けると嬉しいです!↓
![]()
にほんブログ村


コメント