S&P500チャート新発見！？長期トレンド以外の小さな周期変化！

はじめに

本記事のモチベーション

S&P500指数にはどのような印象をお持ちですか？

きっと多くの方が（私も含め）右肩上がりしている有能な指数だと思っているはずです。

ただ、皆さんご存知の通り、長期的に見れば右肩上がりしている指数ですが、短期的に見ると上昇したり下降したりといった細かい変動がありますよね。

今回はその細かい変動が何かしらの傾向があるかどうかに着目しています。

具体的に言うと、細かい上昇や下降の傾向は周期的な変化（何年単位で繰り返されているか）をしているかどうかを調べようとしています。

これを調べることによって、どういうメリットがあるでしょうか？

例えば、５年周期が存在すると仮定します。

2015年から上昇をはじめ、2018年に一気に下落するパターンの周期だとすると（この仮定だと各５年前の2010年と13年にも似たような変化があったはず）、2020年から上昇を始めたものの、2023年に大きく下落すると予測できます。

本当にそのような動きをしないとしても、暴落（暴騰なら別にいいけど）に対する注意点を知っているのと知らないのでは、大きな違いですよね。

長期的な変動はわかっている話ですが、細かい変動にも何かしら規則的な周期が存在しているとすると、このように投資をする上で役立つかもしれないし、何より面白くないですか？

前回の復習

前回は、25年のデータで３〜４年周期があるのではないかと結論づけました。

しかし、３〜４年ってかなりざっくりだな。。。と思ったため、もう少し詰めようと思います。

実は、25年間で7.2個の周期があったと表現することができません。

7.2個の周期は、７個の周期の要素として折り込まれてしまいます。

この点を改善するには結構難しいのですが。。。

今回は小数点以下の周期をしっかり反映させるため、今回はデータを使用する年数を少しずつ変化させて計算していくことにします。

データ・手法

使用データ

今回使用するS&P500指数のデータはStooqから取得した終値を使用しました。

期間は2020年12月31日までを使用しました。

24年間の場合は1997年から、23年間の場合は1998年からというように、古いデータを削除して該当年数としています。

今回は、20年間〜24年間と前回調べた25年を使用しています。

データの種類	取得元	内容
S&P500指数	Stooq	終値

手法

過去記事と手法が全く一緒のため、理解している方は飛ばして結果まで進んでください。

S&P500指数がどのような周期を持っているかを調べる手法として、FFT:fast Fourier transformを使用しました。

FFTの概要とFFTを実行するまでの前処理

FFTを簡単に説明すると、どの周期帯が卓越しているかを調べる手法です。

FFTの説明の記事をご覧いただければ、何がしたいかを大体理解できるかと思います。

FFTを計算する上で、生データをそのまま使うわけにはいかないため、以下の処理を実施した後にFFTを計算しました。

1. 不足データの線形補間
2. 線形トレンドの除去
3. テーパリング

それぞれについて物凄く簡単に説明します。

この内容について知らなくても結果は理解できると思うので、興味がない方は結果まで読み飛ばしてください。

スポンサーリンク

線形補間

線形補間とは、空白データの穴埋めをすることです。

株価は基本的に土日のデータが存在しません。

そのデータを線形的に埋めます。

どういうことかというと、金曜日の株価が200円、月曜日の株価が500円だったとすると、

金曜日と月曜日の株価の差額300円を金→土、土→日、日→月に均等に埋め合わせます。

そのため、100円ずつ増やせば良いので、株価はそれぞれ土：300円、日：400円になるという計算です。

それを株価が存在しない日時全てで実行しました。

線形トレンド除去

線形トレンドの除去とは、長期的な変動を取り除く作業です。

この処理をする理由は、既に分かっている長期的な上昇傾向が結果に反映されても全く意味がないからです。

実際にしている処理は、最小二乗法が・・・とか説明が厄介なので、今回は割愛します。

テーパリング

テーパリングとは、隣接する周波数帯への漏れを軽減させる処理のことです。

この処理をする理由は、スペクトルの漏れを減らす（過大評価させない程度に思ってください）ためです。

具体的にどういうことをするかというと、データの両端の値を０に近づけます。

FFTでは、データの波形が連続する（xxxx-2020年のデータが永遠に続いている）ことを仮定して計算するため、データの始めと終わりの値が一致していなければいけません。

言い換えると、2020年12月31日データの次がxxxx年のはじめのデータになるため、その２点の不連続性をなくすために実施する処理となります（理解できたかな。。。）。

その処理として、今回は、ハミングテーパーを用いました。

株価の値にある関数を掛けることによって実現します。

（テーパリングの計算は見延さん＠北大のサイトを参考にしました）

FFTの注意点

今回使用したnumpyのFFTは、データ数が２のべき乗を推奨（もしかすると必須）しています。

本記事でのデータ数は、20数年×日数で２のべき乗とは程遠いデータ数になっています。

その点は予めご了承ください。

結果

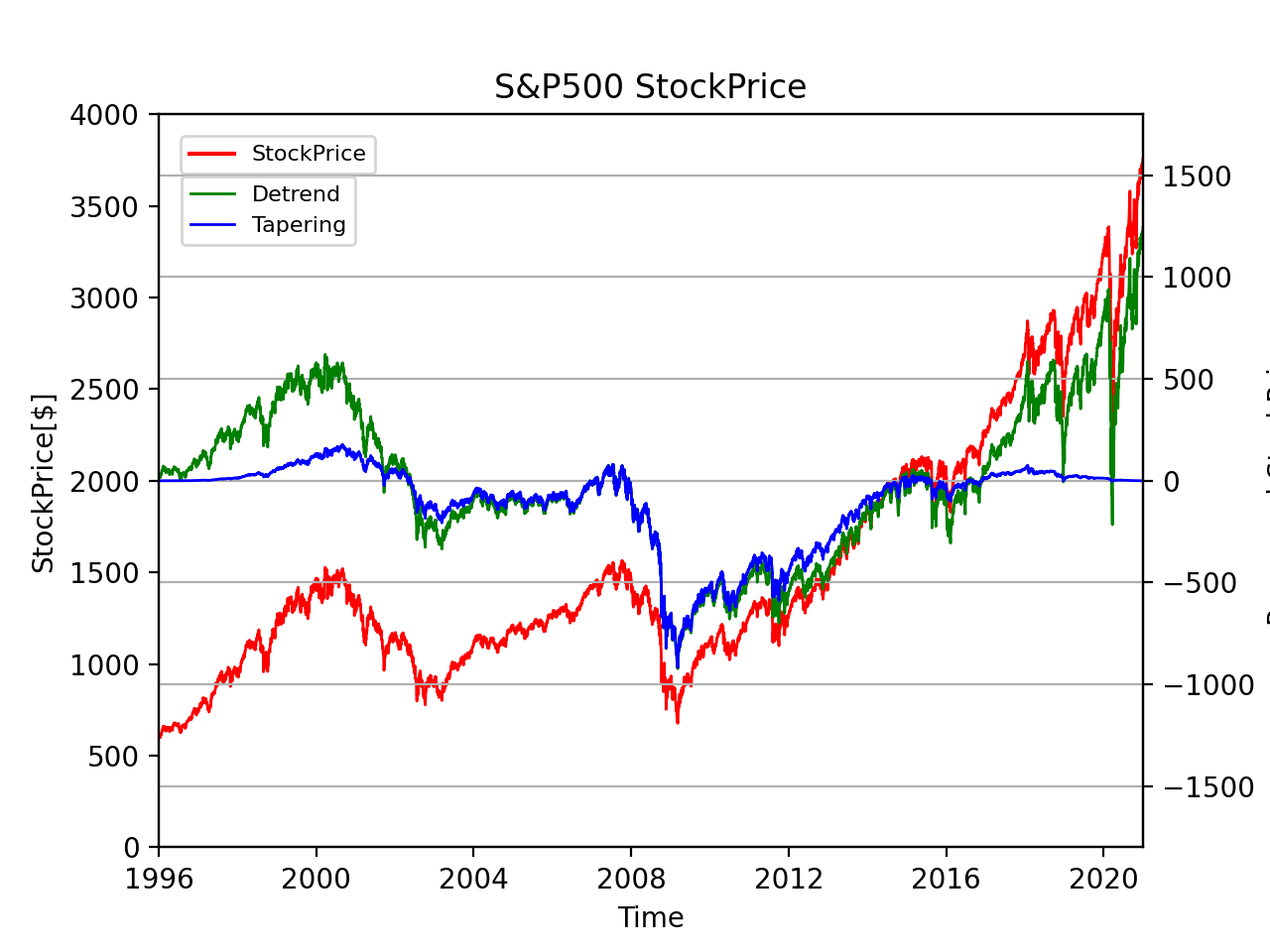
まず、S&P500指数やFFTの前処理をしたデータが（25年間のみ）どのような値になっているかを確認します。

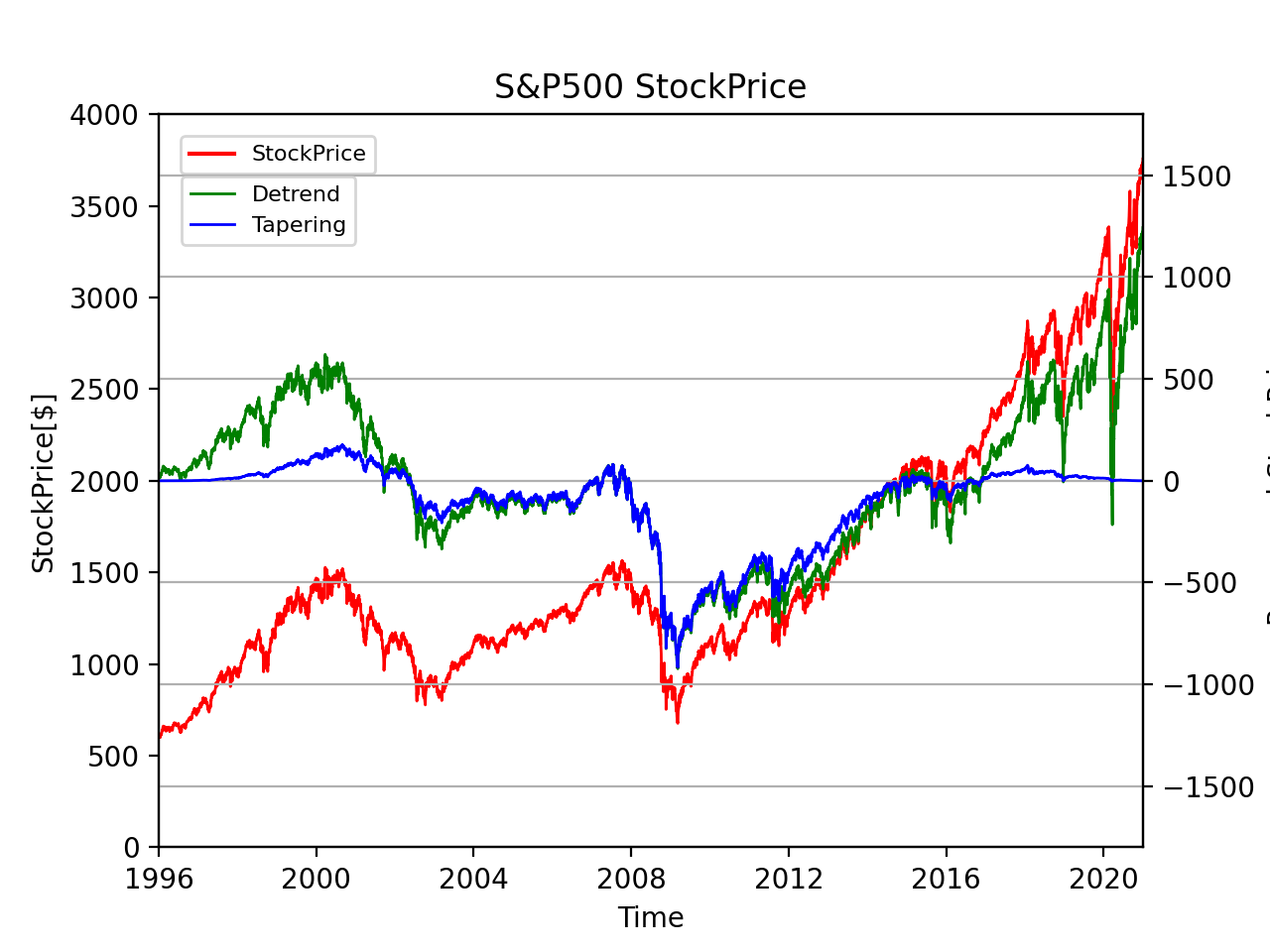
このグラフは、線形補間したS&P500指数、線形補間＋線型トレンド除去したS&P500指数、線形補間＋トレンド除去＋テーパリングしたS&P500指数の経年変化です。

線形補間＋トレンド除去は線形補間と比べて長期的な上昇傾向が抑えられて、線形補間＋トレンド除去＋テーパリングは線形補間＋トレンド除去と比べて両端が０に近づいており、理想的な処理ができています。

線形補間＋トレンド除去＋テーパリングの値を使って、FFTを計算していきます。

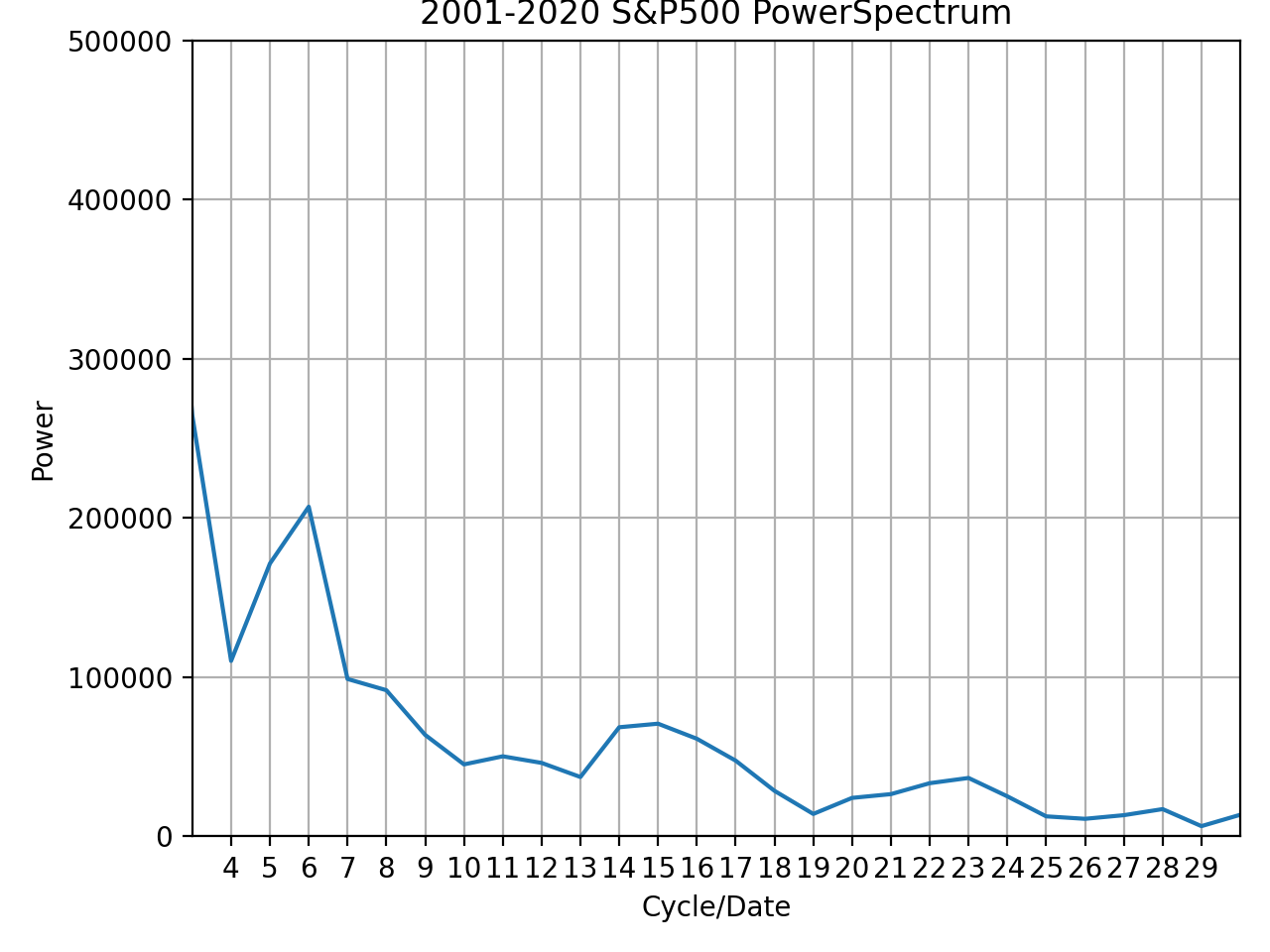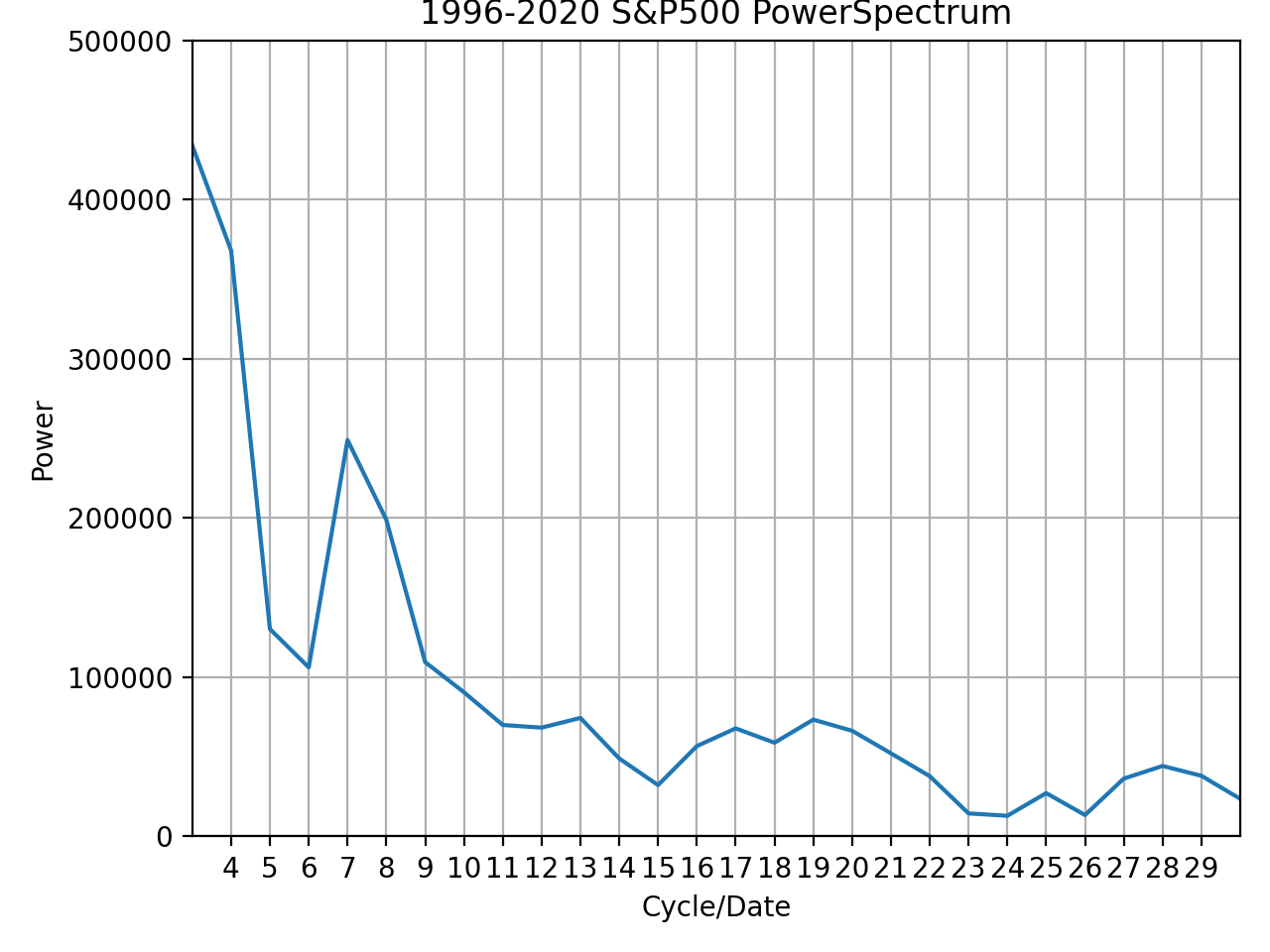
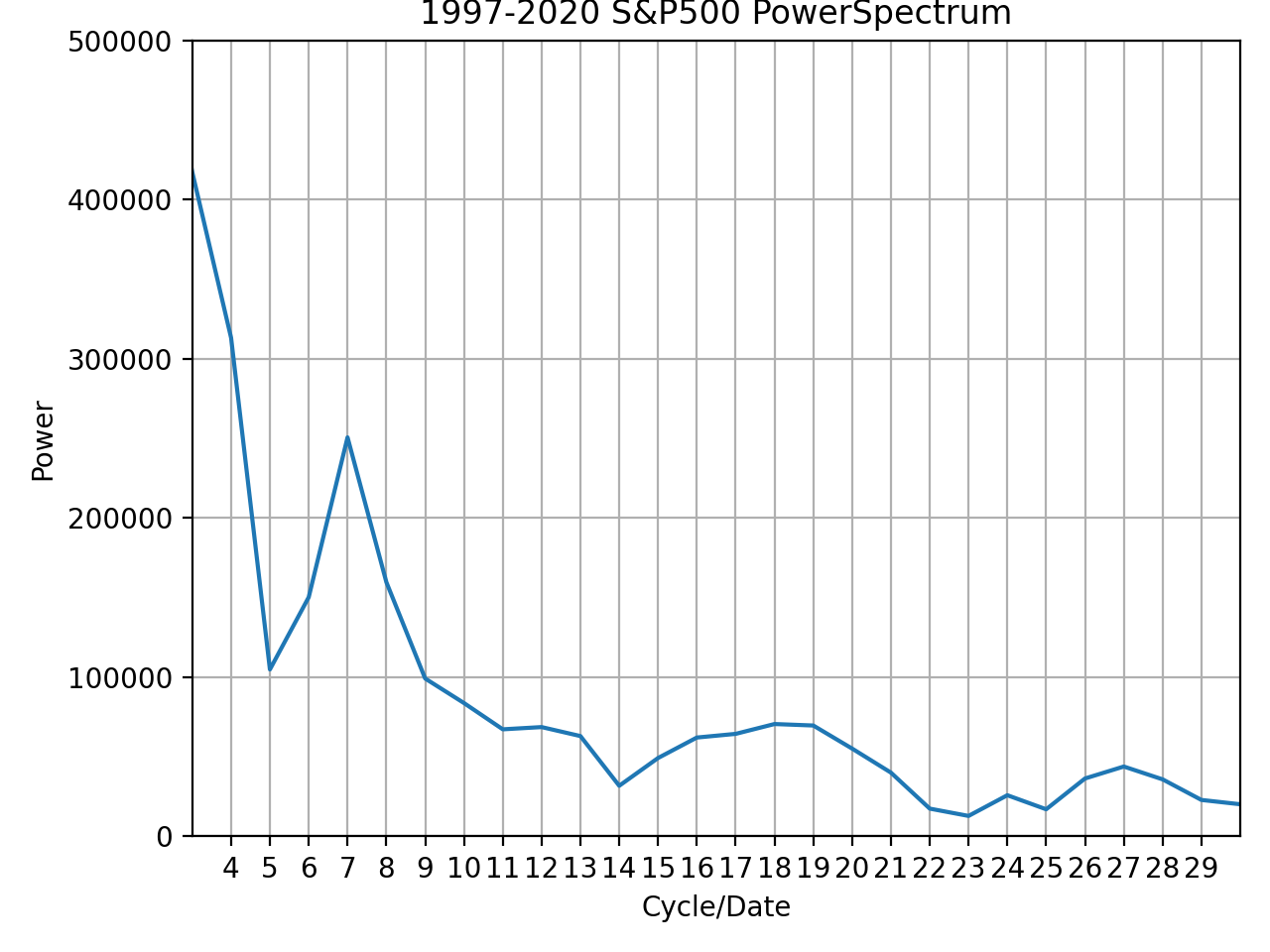
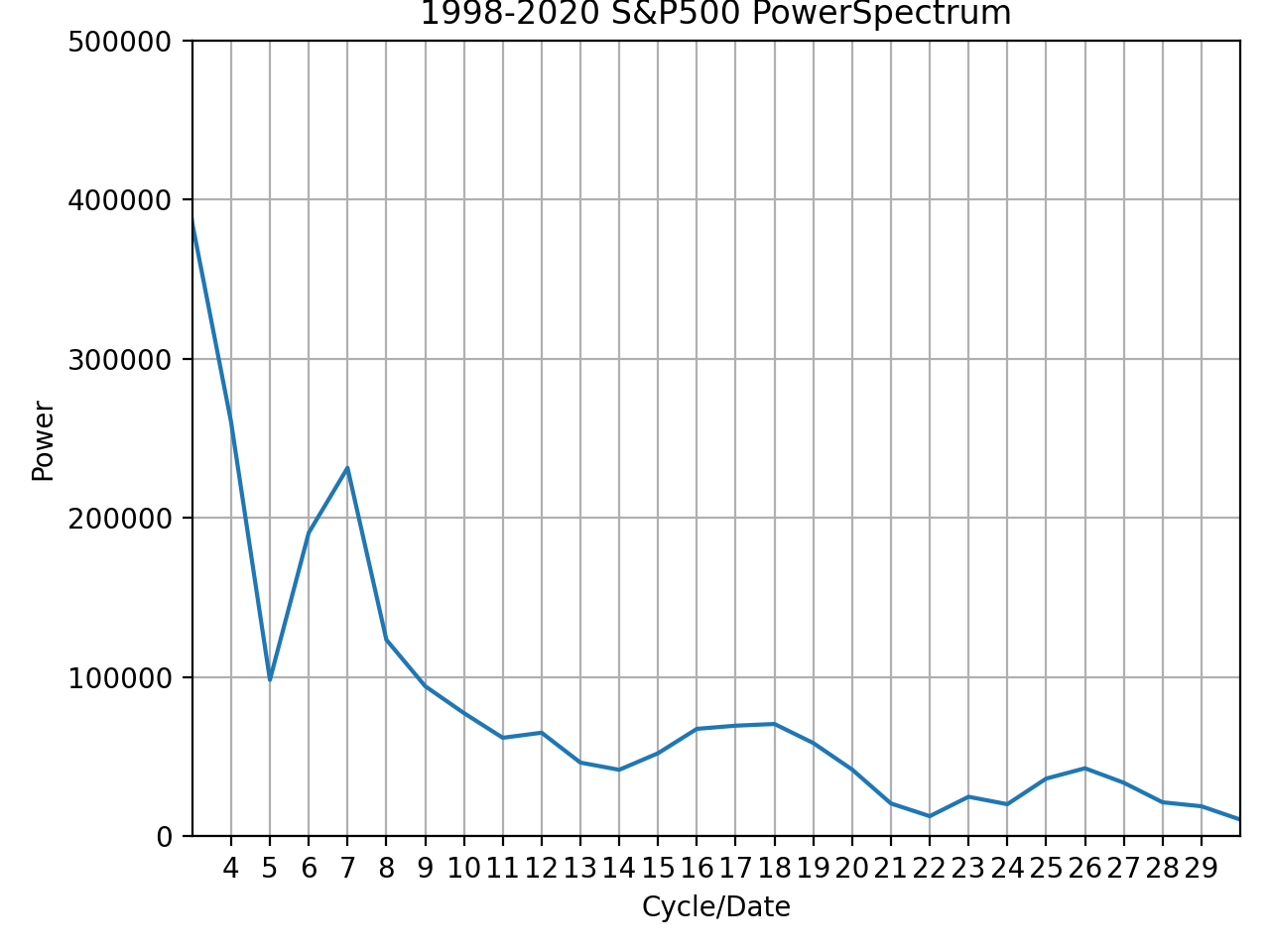
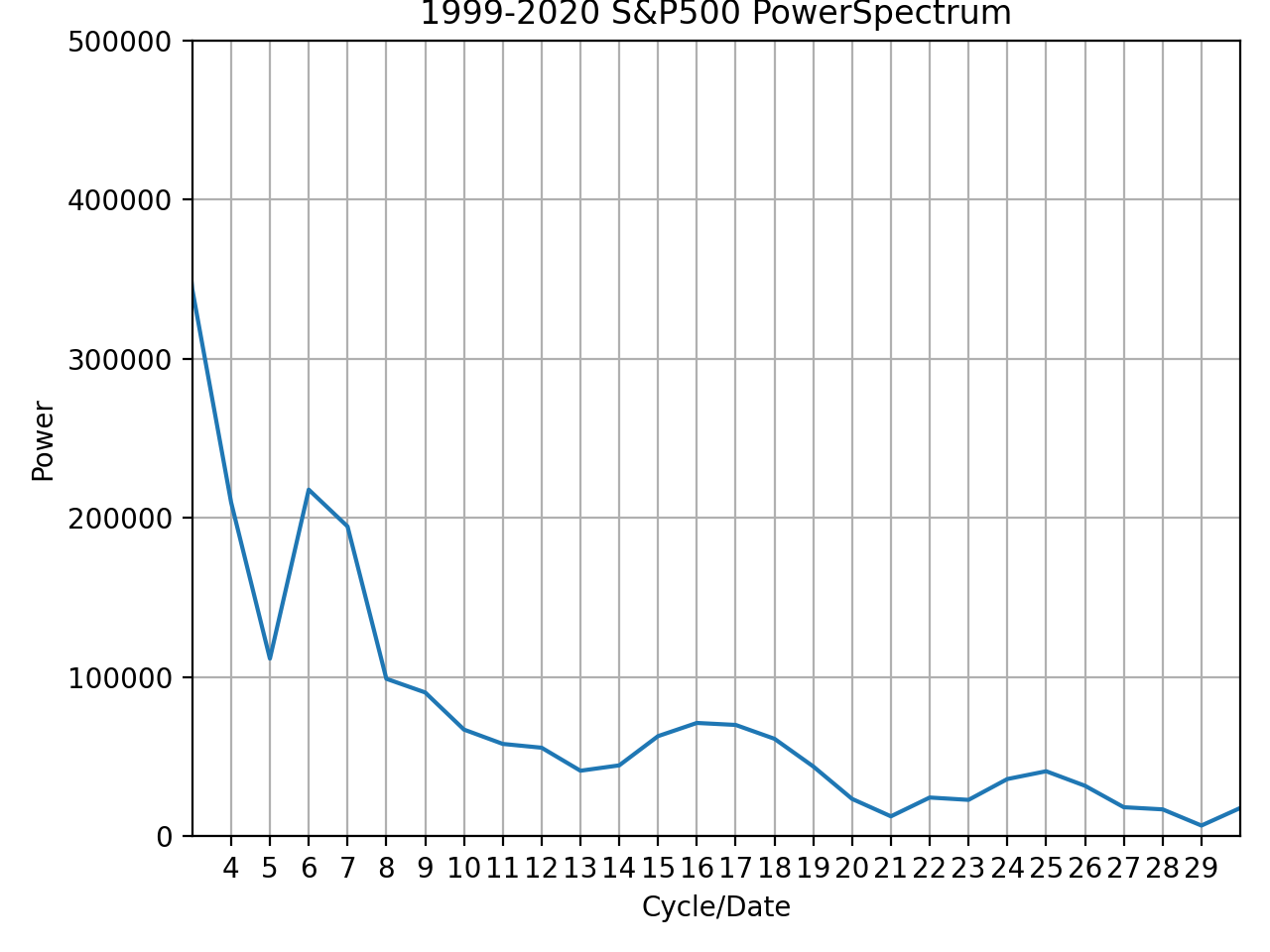
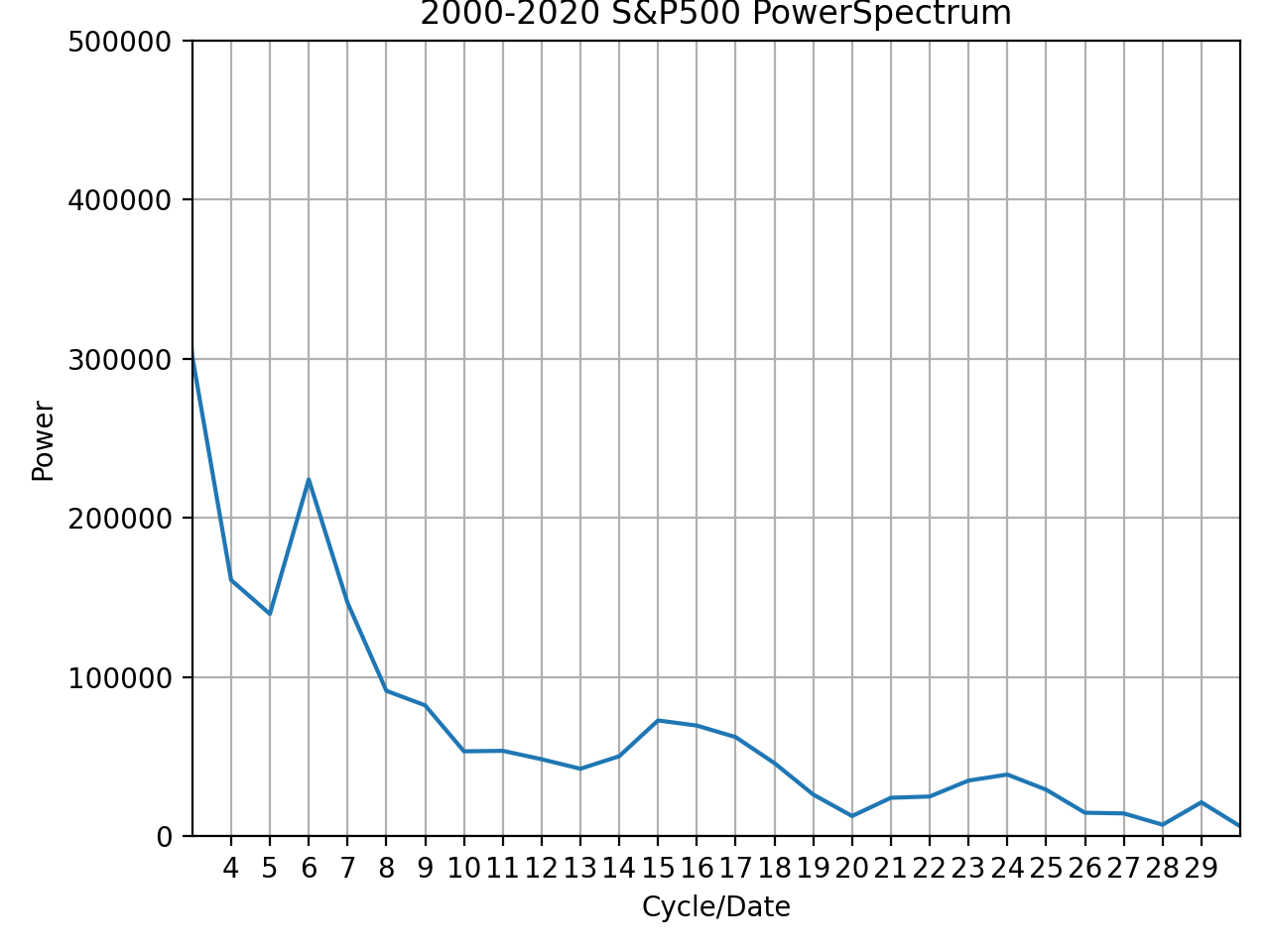
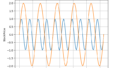
FFTを計算した結果がこのグラフとなります。

このグラフは、

• 横軸：xxxx-2020の該当年数における周期の数
• 縦軸：パワー

を示しています。

このグラフの見方が難しいので説明すると、
横軸が６→24年で６個の周期がある＝４年周期
横軸が24→24年で24個の周期がある＝１年周期
といった見方をします。

上記の図はそれぞれ期間が異なっており、左上:1996-2020年の25年間、右上:1997-2020年の24年間、左:1998-2020年の23年間、右:1999-2020年の22年間、左下:2000-2020年の21年間、右下:2001-2020年の20年間です。

また、縦軸はパワー（パワースペクトル（密度））となっており、大きいほどその周期帯が卓越していることを示しています。

今回はいずれもデータが多いので、ノイズ（評価されない周期が近くの周期帯の評価として反映されること）がかなり大きい可能性があります。

そのため、周辺の周期よりもその周期が卓越している場合（10の場合、10前後の振幅よりも10がはるかに大きいか）で卓越していると評価します。

これらの図を見て、綺麗に値が飛び出ているところを判断します。

上記の観点から見ると、統計的な検定をしなければいけないものの、24年間の７と21年間の６で周期が卓越していると言えると思います。

それぞれを計算（周期の数/年数）すると、約3.42、3.5となります。

そのため、過去データを振り返ると約３年半の周期が卓越していそうだと言うことがわかりました。

今回の結果を踏まえると、長期的な上昇傾向があるにしても、３年半ごとに何かしらの小さな変動を繰り返しているという可能性があるということです。

もしかすると、３年半前に起こった傾向の変動が、今もう一度似たように起こるなんてこともあるのかもしれませんね。

スポンサーリンク

注意点

今回の調査は過去20〜24年間に絞って解析をしました。

なお、これは過去の話であって、将来が同様になると言うことではないため、その点はご理解ください。

ただし、過去に小さめではあるものの3.5年周期といった変動があるという事実は証明されました。

この結果を踏まえて、これから私が知りたいのは以下ですかね。

• どのような原因（要因）で小さな3.5年周期が起こっているのか
• この3.5年周期でどのような変動をしているのか（いつ頃上昇していつ頃下落するのかなど）

上記を詰めることができれば、将来的にも続くような傾向になるのかといった、かなり参考になる情報になり得るのではないかと思っています。

これを調べる方法がまた難しいんですけどね。。。

まとめ

↓とりりんを応援して頂けると嬉しいです！↓

にほんブログ村