こんにちは、とりりんです。
今日は、みんなが大好きな指数であるS&P500に一定の周期が存在するかを調べました!
- 米国株に投資している方
- 投資に興味がある方
- 米国経済に興味がある方
- 統計に興味がある方
過去のお話とはいえ、個人的にはこの結果を知っておいて損はないと思います。
最後までご覧いただけると嬉しいです!
はじめに
S&P500指数にはどのような印象をお持ちですか?
きっと多くの方が(私も含め)右肩上がりしている有能指数だと思っていると思います。
ただ、皆さんご存知の通り、長期的に見れば右肩上がりしている指数ですが、短期的に見ると上昇したり下降したりといった細かい変動がありますよね。
長期的な変動はわかっている話ですが、細かい変動にも何かしら規則的な周期が存在しているとすると、投資をする上で役立つかもしれないし、何より面白くないですか?
そこで、今回はS&P500指数に周期的な変化が存在しているかどうかを調査してみようと思います!
データ・手法
使用データ
今回使用するS&P500指数のデータはStooqから取得した終値を使用しました。
期間は1996年1月2日から2020年12月31日までの25年間です。
| データの種類 | 取得元 | 内容 |
| S&P500指数 | Stooq | 終値 |
|---|
手法
S&P500指数がどのような周期を持っているかを調べる手法として、FFT:fast Fourier transformを使用しました。
FFTを簡単に説明すると、どの周期帯が卓越しているかを調べる手法です。
気温は本当に日周期なのかの記事をご覧いただければ、何をしたいかを大体理解できるかと思います。
FFTは離散フーリエ変換を高速で計算するアルゴリズムです(理解する必要はないです、私もそんなにわかってない)。
FFTを計算する上で、生データをそのまま使うわけにはいかないため、以下の処理を実施した後にFFTを計算しました。
- 不足データの線形補間
- 線形トレンドの除去
- テーパリング
それぞれについて物凄く簡単に説明します。
この内容について知らなくても結果は理解できると思うので、興味がない方は結果まで読み飛ばしてください。
スポンサーリンク
線形補間
線形補間とは、空白データの穴埋めをすることです。
株価は基本的に土日のデータが存在しません。
そのデータを線形的に埋めます。
どういうことかというと、金曜日の株価が200円、月曜日の株価が500円だったとすると、
金曜日と月曜日の株価の差額300円を金→土、土→日、日→月に均等に埋め合わせます。
そのため、100円ずつ増やせば良いので、株価はそれぞれ土:300円、日:400円になるという計算です。
それを株価が存在しない日時全てで実行しました(1996年1月1日はサボりました、許してください)。
線形トレンドの除去とは、長期的な変動を取り除く作業です。
この処理をする理由は、既に分かっている長期的な上昇傾向が結果に反映されても全く意味がないからです。
実際にしている処理は、最小二乗法が・・・とか説明が厄介なので、今回は割愛します。
テーパリング
テーパリングとは、隣接する周波数帯への漏れを軽減させる処理のことです。
この処理をする理由は、スペクトルの漏れを減らす(過大評価させない程度に思ってください)ためです。
具体的にどういうことをするかというと、データの両端の値を0に近づけます。
FFTでは、データの波形が連続する(1996-2020データが永遠に続いている)ことを仮定して計算するため、データの始めと終わりの値が一致していなければいけません。
言い換えると、2020年12月31日データの次が1996年1月2日のデータになるため、その2点の不連続性をなくすために実施する処理となります(理解できたかな。。。)。
その処理として、今回は、ハミングテーパーを用いました。
株価の値にある関数を掛けることによって実現します。
(テーパリングの計算は見延さん@北大のサイトを参考にしました)
FFTの注意点
今回使用したnumpyのFFTは、データ数が2のべき乗を推奨(もしかすると必須)しています。
本記事でのデータ数は、25年×日数で2のべき乗とは程遠いデータ数になっています。
その点は予めご了承ください。
結果
まず、S&P500指数やFFTの前処理をしたデータがどのような値になっているかを確認します。
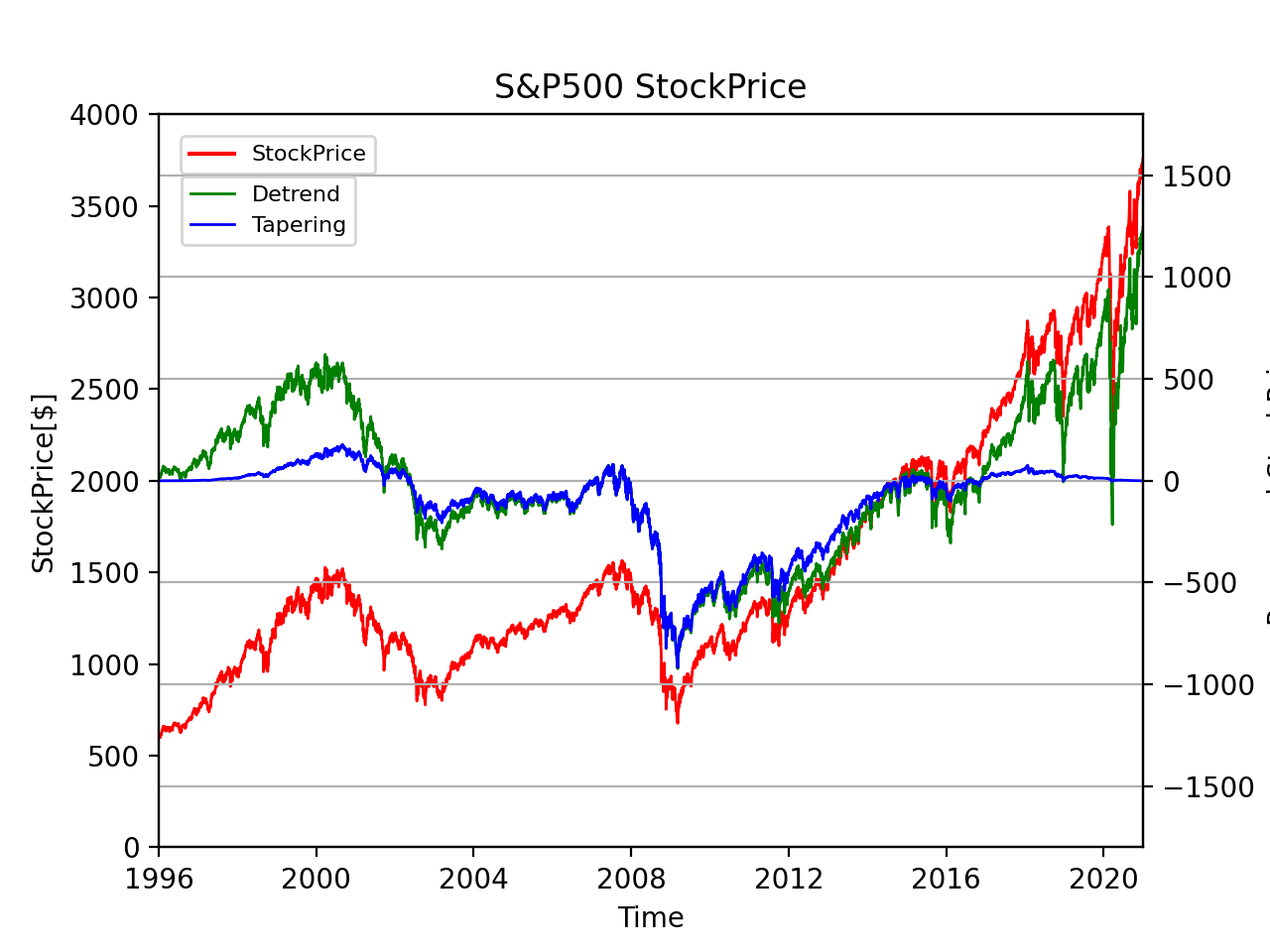
このグラフは、線形補間したS&P500指数、線形補間+線型トレンド除去したS&P500指数、線形補間+トレンド除去+テーパリングしたS&P500指数の経年変化です。
線形補間+トレンド除去は線形補間と比べて長期的な上昇傾向が抑えられて、線形補間+トレンド除去+テーパリングは線形補間+トレンド除去と比べて両端が0に近づいており、理想的な処理ができています。
線形補間+トレンド除去+テーパリングの値を使って、FFTを計算していきます。
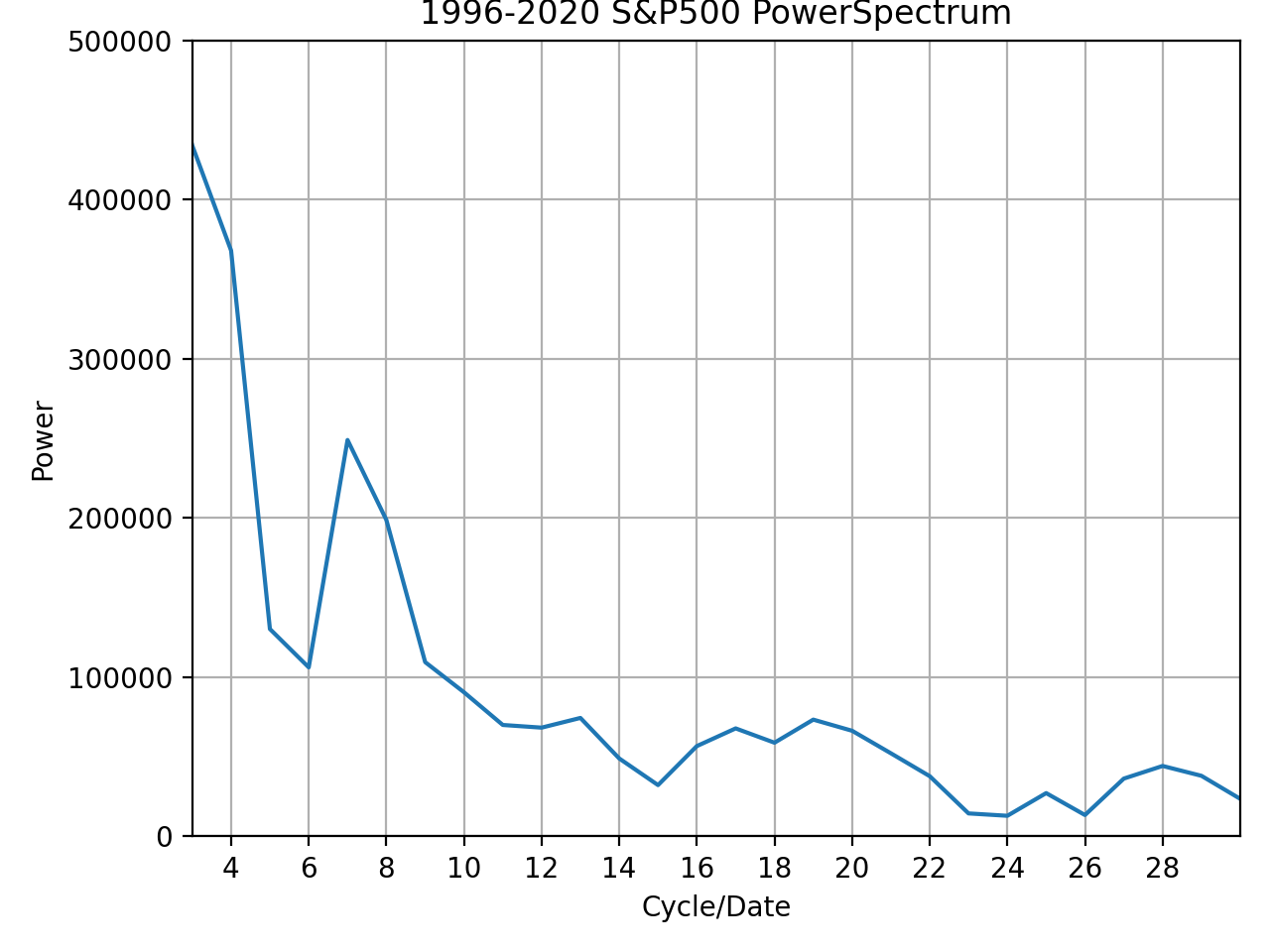
FFTを計算した結果がこのグラフとなります。
このグラフは、
- 横軸:1996-2020の25年間での周期の数
- 縦軸:パワー(大きいほど周期が卓越)
このグラフの見方が難しいので説明すると、
横軸が5→25年で5個の周期がある=5年周期
横軸が25→25年で25個の周期がある=1年周期
といった見方をします。
また、パワー(パワースペクトル(密度))となっており、大きいほどその周期帯が卓越していることを示しています。
今回は15年とデータが多いので、ノイズ(評価されない周期が近くの周期帯の評価として反映されること)がかなり大きい可能性があります。
そのため、周辺の周期よりもその周期が卓越している場合(10の場合、10前後の振幅よりも10がはるかに大きいか)で卓越していると評価します。
上記の観点から見ると、隣接し合っている+統計的な検定をしなければわかりませんが、7と8で周期が卓越していると言えると思います。
25年で7か8個の周期が存在しているということは、約3〜4年周期が卓越していそうだと言うことです。
今回の結果を踏まえると、長期的な上昇傾向があるにしても、3, 4年ごとに何かしらの小さな変動を繰り返しているという可能性があるということです。
もしかすると、3, 4年前に起こった変動が、今もう一度似たように起こるなんてこともあるのかもしれませんね。
スポンサーリンク
注意点
今回の調査は過去25年間に絞って解析をしました。
1961年からの60年間で同様に解析しましたが、95年までの35年間は長期的観点での変動幅がかなり小さかったため、良い結果が得られませんでした。
なお、これは過去25年間での話であって、将来が同様になると言うことではないため、その点はご理解ください。
歴史は繰り返されるというので、知ってて損する内容ではないとは思いますが。
まとめ
今日は、S&P500指数に長期傾向以外の小さな周期的な変動があるかどうかを調べました!
FFTなんてわけわからん!と思ったと思います。笑
今回言いたいのは一言だけです!
それは、過去25年のデータを見ると、長期的な上昇傾向以外に、約3, 4年周期の小さな繰り返される傾向が見られることがわかったということです。
これからもこのような調査を続けていくつもりなので、チェックしていただけると嬉しいです!
難しい内容でしたが、最後までご覧いただき、ありがとうございました!
↓とりりんを応援して頂けると嬉しいです!↓
![]()
にほんブログ村

コメント