こんにちは。とりりんです。
今回は移動性高気圧を相関係数を使って解析的に調査してみたいと思います。
前回よりも単純にできるじゃん!と思って実行した改良版です。
こんなことが知りたい方向けです。
- 移動性高気圧を知りたい方
- 天気とデータ分析に興味がある方
- プログラミング初心者の方
- この話題を面白そうと思った方
是非最後までご覧ください。
おさらい
移動性高気圧とは、文字どおり移動する高気圧のことで、春(4, 5月)と秋(10, 11月)に顕著に現れる現象のことです。
移動性高気圧がsinカーブのような同じような変動を一定の周期でしていた場合、周期にあたる場所でラグ相関係数が高くなるはずです。
そこで、気圧データからラグ相関係数を計算することで移動性高気圧の存在が分かるかどうかを調べました。
使用データ
今回は気象庁から福岡1日ごとの現地気圧と海面気圧データを使用しました。
前回との違いは福岡と秋田の2地点ではなく、福岡のみ使用している点です。
期間は2010年から2021年まで使用しましたが、結果が良かった年(前回と同じく2017年でした)のみ出します。
全く同じデータでラグ相関係数を計算するため、ラグ=0の時の相関係数は1になります。
また、前回と同じくラグを0〜14日で、期間を季節ごとに分けて計算しました。
移動性高気圧は冒頭でお話した通り4, 5月と10, 11月に顕著なのですが、今回は下記で季節を分類しています。
- オールシーズン:1〜12月
- 春:3〜5月
- 夏:6〜8月
- 秋:9〜11月
- 冬:12〜2月
スポンサーリンク
結果・考察
量が多いので詳しくはお見せしませんが、年によってすごく違いがありました。
うまくいった年やそうでもない年など様々ありますが、結果が1番よかった2017年を紹介します。
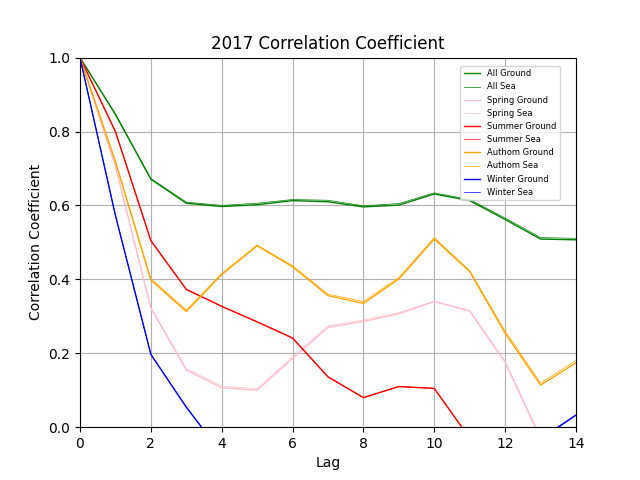
この図は2017年の季節(色)ごとにラグ(横軸)ごとの相関係数(縦軸)を示しています。
相関係数の範囲は本来-1〜1ですが、今回は見やすさ重視で負の値は描画から除外しました。
季節はそれぞれ全季節、春、夏、秋、冬を示しています。
なお、太い線が現地気圧、細い線が海面気圧の相関係数を示していますが、そんなに変わらないので気にしなくて結構です。
結果を見れば一目瞭然ですが秋でより顕著な良い結果が得られました。
ラグ5日と10日で相関係数の極大があり、移動性高気圧が5日周期であることがわかります。
ただ春は秋と比べて全体的にイマイチでした。
3月を含めたのが良くなかったのか、そこまで綺麗に現れないのか…。
因みに、前回の福岡と秋田で実行した場合は下記になります。
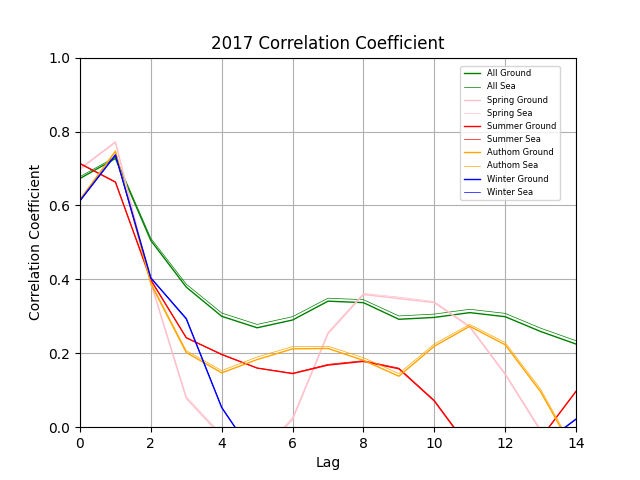
違いが一目瞭然。正直ここまで綺麗に出てくるとは思いませんでした。
スポンサーリンク
まとめ
今回は気圧データを使って移動性高気圧の存在を確かめてみました。
今回の話をまとめると下記のようになります。
- 前回うまくいかなかったので福岡データのみでラグ相関を計算
- 2017年秋に明瞭な5日周期発見!
- 一方で春はイマイチ
- 原因は3月が含まれているから?元々秋ほど明瞭に見えにくい?
今回の結果は元々考えられる3〜4日周期と近いことから、完全に移動性高気圧を示した結果だと言えますね。
最後までご覧いただき、ありがとうございました!
Python
GitHub
Qiita
↓とりりんを応援して頂けると嬉しいです!↓
![]()
にほんブログ村



コメント